Problem Solving and Search

This is a 1st-year course in the UvA's BSc Artificial Intelligence programme. It provides an introduction to algorithmic thinking and basic problem solving techniques in AI. Special emphasis is put on search algorithms and their implementation in the declarative programming language Prolog. This website provides some general information about the course as well as access to the lecture notes and the slides used during classes. For day-to-day information, including homework assignments, please refer to the UvA Canvas system.

Lecturer: Ulle Endriss (ILLC, University of Amsterdam)
Textbook: I. Bratko. Prolog Programming for Artificial Intelligence. 4th edition, Addison-Wesley Publishers, 2012.
Lecture Notes: An Introduction to Prolog Programming (errata)
Slides: Introduction | Prolog | Sorting | Search
Datanose: schedule and room information
Canvas: homework assignments, regulations, and more
SWI-Prolog: download and documentation

Examples. During weekly homework assignments you will encounter a wide variety of exciting and challenging problems in AI and you will learn how to solve them by applying the fundamental principles and techniques taught during lectures. Below are some representative examples.

In the Letters Game, familiar from the famous television game show Countdown (also known as Cijfers en Letters), the contestants have to construct the longest possible word from a given list of nine letters. For example, for the list [r,d,i,o,m,t,a,p,v], a strong answer would be 'dioptra'.

You will learn that it is fairly easy to write a program that beats any human player hands down at this game.

In the Numbers Game, also part of Countdown, contestants are given one large and six smaller numbers. They have to construct a mathematical expression using only the small numbers to get as close as possible to the large one. For example, for the list [25,50,75,100,3,6] and target 444, a perfect solution would be 3*(50+100)-6.

Although much more challenging than the Letters Game, you will still learn how to write a program that can beat the very best human contestants also at this game.

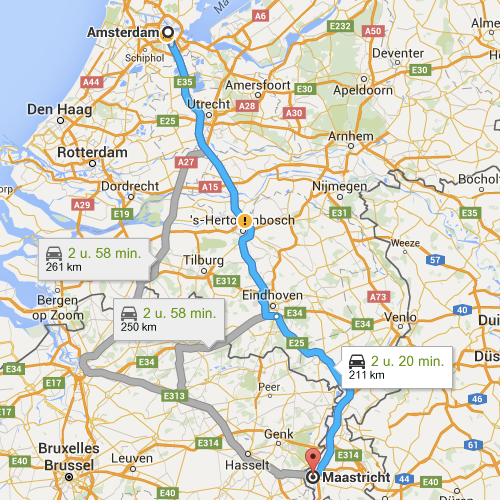
At the heart of online travel recommendation services such as the one offered by Google are algorithms for finding the shortest path between two points on a map.

You will learn how to write a program to find the shortest route between any two major cities in the Netherlands.

In the Treaty of Rome (1957) the six founding members of the European Union fixed the voting rule to decide on proposals in the European Council. To pass, a proposal had to get at least 12 votes. France, Germany, and Italy each had 4 votes; Belgium and the Netherlands each had 2 votes; and Luxembourg had 1 vote. Is that fair?

Treaty of Rome Signing Ceremony (source: Wikipedia)

You will learn how to write a program to compute the voting power of each country, so as to be able to discuss such questions of fairness systematically.

The game of Tic-Tac-Toe is played on a 3x3 grid by two players who alternate in putting marks on the grid. The player who first manages to put three of her marks in either a row, a column, or along one of the diagonals wins the game.

You will learn how to write a program to compute your optimal move in any given situation and never lose a game of Tic-Tac-Toe again.

In 1742, in a letter to the famous mathematician Leonhard Euler, Christian Goldbach conjectured that every even number greater than 2 is the sum of two prime numbers. To date, no mathematician has been able to prove that Goldbach's Conjecture really is true for all even numbers.

You will learn how to write a program that confirms the conjecture for all numbers up to 10,000 in under 1 second.

Suppose a robot starts in the upper lefthand corner of the maze shown below and wants to move to the lower righthand corner...

You will learn how to write a program to help the robot find its way through this and any other kind of maze.

The Eight Queens Problem is a famous chess problem asking you to place eight queens on a chess board in such a way that none of them can attack any of the others.

You will learn how to write a program that solves the problem in under 10 milliseconds. And it will enumerate all possible solutions in under 100 milliseconds.

A farmer wants to get a fox, a chicken, and a bag of grain across a river, but at most one of these will fit in his boat besides himself. He mustn't leave the fox and the chicken on their own, nor the chicken and the grain, for fear of one of them getting eaten by the other. Is it possible to move everything safely to the other side?

You will learn how to write programs to solve puzzles of this kind in a systematic fashion.

Why Prolog? Prolog is one of the classical programming languages developed specifically for applications in AI. In Prolog you can write very short and elegant programs to solve nontrivial problems. For example, the nine problems described above on average require fewer than 30 lines of code. (Well, to be completely precise, for the route-finding application we also need access to a database of cities and roads in the Netherlands; and for the Letters Game we also need access to a lexicon.) The course will focus on the general patterns underlying the solutions to such problems. For example, finding a perfect answer in the Numbers Game, helping the robot through the maze, and solving the Eight Queens Problem can all be realised with the help of the same kind of basic search algorithm.

Topics. The course covers the following topics:

Basic features of the Prolog programming language, including lists, arithmetic expressions, operators, cuts, and negation-as-failure; as well as a few additional features, such a file handling, dynamic predicates, and collecting all answers for a given goal. The basic concept of programming by means of recursion will take on a central role. We will also discuss the way in which Prolog works, including the concepts of matching and backtracking.
Basic aspects of algorithm design, including the formal analysis of the time and memory requirements of algorithms using the Big-O notation. Our initial examples will concern the design of sorting algorithms, such as bubblesort and quicksort.
Search algorithms, including depth-first search, breadth-first search, iterative deepening, heuristic-guided search using the A* algorithm, and adversarial search using the minimax algorithm and alpha-beta pruning. We are also going to introduce a general approach for modelling a wide range of search problems using the so-called state-space representation.