Compact Peaucellier cell

The Peaucellier cell is a linked mechanism that converts a motion to its inverse curve. If the original motion is a circle, then the inverse is also a circle. If the motion is a circle through the origin, then the inverse is a circle of infinite radius, which is (locally at least) a straight line. So the Peaucellier cell can be used to convert a rotary motion to a linear motion.

For a long time, it was thought that a linkage mechanism doing that conversion could not exist. When it was found, it was used in some of the early steam engines. For more on the history of this and other linkages, click here.

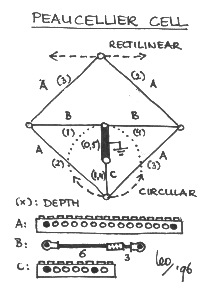
For the general Peaucellier cell, the struts 'A' should be of equal length, and so should the struts 'B', but there is no requirement on their relative lengths. I wanted to make a compact and symmetrical version of the cell, specifically for the conversion of rotary to linear motion, with everything taking place in the square of struts 'A', nicely symmetrically. With the long struts 'A' of length 14 between the connection points (indicated in dark), the struts 'B' need to be of length 14/sqrt(2) = 9.899, which is just short of 10. I found that by connecting axles as in the sketch, I obtain a length that is just about right. The numbers in brackets denote 'layers' of the mechanism. The thick bar is affixed to the world.

Here is a Cinderella/JAVA interactive demo, demonstrating the construction and its movement, and another JAVA applet

And the above sketch has been converted into an actual model by Philippe Hurbain. Here is his movie of the functioning:


You can use this when you want to guide a straight motion, but your 12-long LEGO axles are too short. (Actually, there are better solutions for that problem, I will post them at some time...)

000313