De quantummechanische beschrijving van de fysische toestand waarop een
deeltje zich op een bepaald tijdstip bevindt, is niet - zoals in de
klassieke fysica - door zijn positie en snelheid te specificeren, maar
door de golffunctie 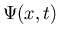 te geven. Deze golffunctie is
complex, hetgeen betekent dat hij in elk punt door een grootte
(absolute waarde)
te geven. Deze golffunctie is
complex, hetgeen betekent dat hij in elk punt door een grootte
(absolute waarde) 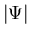 en een fase factor (een hoek) wordt vastgelegd,
d.w.z. door een vector in een tweedimensionaal vlak. De grootheid
en een fase factor (een hoek) wordt vastgelegd,
d.w.z. door een vector in een tweedimensionaal vlak. De grootheid
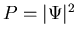 correspondeert met de waarschijnlijkheidsdichtheid om het
deeltje ten tijde t op plaats x aan te treffen wanneer deze in de
toestand
correspondeert met de waarschijnlijkheidsdichtheid om het
deeltje ten tijde t op plaats x aan te treffen wanneer deze in de
toestand 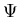 zit.
zit.
De fasefactor is niet direct meetbaar, maar maakt
het enerzijds mogelijk om specifiek quantummechanische eigenschappen
aan deeltjes toe te kennen en geeft anderzijds aanleiding tot de
interferentie effecten (het befaamde dubbele spleet experiment) die de
fysische uitdrukking zijn van de deeltje-golf dualiteit.
De intrinsieke quantummmechanische eigenschappen die geen klassiek
analogon hebben zijn de `spin' of `intrinsiek impulsmoment' en
de 'statistiek' van een deeltje. De spin bepaalt hoe de fase van
een golffunctie verandert als we het deeltje in de ruimte roteren. De
statistiek reflecteert het feit dat in de quantum mechanica identieke
deeltjes niet te onderscheiden zijn. De statistiek van een deeltje
vertelt ons hoe de golffunctie van een toestand die meerdere identieke
deeltjes bevat zich gedraagt onder verwisseling van twee identieke
deeltjes. In drie of meer ruimtelijke dimensies is de spin s heel-
of halftallig, en de statistiek even of oneven, corresponderend met
bosonen en fermionen respectievelijk. Bij de verwisseling
van twee identieke fermionen keert de golffunctie van teken om, bij de
verwisseling van tweee identieke bosonen verandert er niets. Dit
relatieve minteken heeft dramatische gevolgen voor de eigenschappen
van systemen die veel identieke deeltjes bevatten, bosonen vinden het
leuk om in dezelfde toestand te gaan zitten en kunnen onder bepaalde
voorwaarden ``condenseren'', fermionen daarentegen kunnen niet in
dezelfde toestand zitten (het uitsluitingsbeginsel van Pauli). Het
laatste verklaard bijvoorbeeld de structuur van het periodiek systeem
waarbij de verschillende electronen in het atoom bij oplopend
atoomnummer meer en meer van de beschikbare toestanden bezetten. De
theoretische verklaring van het experimentele verband tussen spin en
statistiek is een van de successen van de relativistische
quantumveldentheorie.
In twee dimensies ligt de zaak anders, de spin s is niet
gequantiseerd en kan in principe elke reële waarde aannemen. Een
rotatie van het deeltje over een hoek 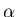 resulteerd in een
rotatie van de golffuntie ( in het complexe vlak) met een hoek
resulteerd in een
rotatie van de golffuntie ( in het complexe vlak) met een hoek 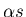 .
Wat betreft de statistiek is de situatie in twee dimensies ook
verschillend. Bij het verwisselen van identieke deeltjes kan men
linksom dan wel rechtsom verwisselen, en deze beide mogelijkheden zijn
in het vlak niet continu in elkaar over te voeren: ze zijn
inequivalent. Het is daarom niet langer noodzakelijk dat de
verwisselingsoperatie (linksom) hetzelfde effect heeft op de
golffunctie als zijn inverse (rechtsom). Anders gezegd, in twee
dimensies hoeven twee opeenvolgende verwisselingen de golffunctie niet
invariant te laten. Dien tengevolge kunnen we in twee dimensies een
continue statistische, periodieke parameter
.
Wat betreft de statistiek is de situatie in twee dimensies ook
verschillend. Bij het verwisselen van identieke deeltjes kan men
linksom dan wel rechtsom verwisselen, en deze beide mogelijkheden zijn
in het vlak niet continu in elkaar over te voeren: ze zijn
inequivalent. Het is daarom niet langer noodzakelijk dat de
verwisselingsoperatie (linksom) hetzelfde effect heeft op de
golffunctie als zijn inverse (rechtsom). Anders gezegd, in twee
dimensies hoeven twee opeenvolgende verwisselingen de golffunctie niet
invariant te laten. Dien tengevolge kunnen we in twee dimensies een
continue statistische, periodieke parameter 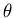 (
(
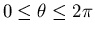 )
introduceren. Waarbij
)
introduceren. Waarbij 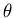 de faseverandering is bij
verwisseling van twee deeltjes. De corresponderende deeltjestypen
worden generiek anyonen genoemd omdat zij `any phase' kunnen
genereren onder verwisseling.
de faseverandering is bij
verwisseling van twee deeltjes. De corresponderende deeltjestypen
worden generiek anyonen genoemd omdat zij `any phase' kunnen
genereren onder verwisseling.
Er is een subtiele generalisatie van het befaamde dubbele spleet
experiment, het Aharonov-Bohm effect, waarbij we ons voorstellen
dat we een perfect afgeschermde zeer lange solenoïde tussen en
parallel aan de spleten plaatsen. Door de stroom in de solenoïde
te variëren genereren we een magnetische flux 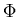 door de
solenoïde parallel aan de spleten. Voor een deeltje met lading
q is het extra faseverschil tussen de bijdragen van de
verschillende spleten gelijk aan
door de
solenoïde parallel aan de spleten. Voor een deeltje met lading
q is het extra faseverschil tussen de bijdragen van de
verschillende spleten gelijk aan 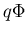 , met het gevolg dat het interferentiepatroon verschuift.
Dit effect laat zien dat de
koppeling aan de vectorpotentiaal
, met het gevolg dat het interferentiepatroon verschuift.
Dit effect laat zien dat de
koppeling aan de vectorpotentiaal 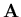 in een veldvrije ruimte
(d.w.z. door een deel van de ruimte waar de electrische en magnetische
velden nul zijn)in de quantumtheorie toch een waarneembaar effect,
n.l. het verschuiven van het interferentiepatroon, kan veroorzaken.
in een veldvrije ruimte
(d.w.z. door een deel van de ruimte waar de electrische en magnetische
velden nul zijn)in de quantumtheorie toch een waarneembaar effect,
n.l. het verschuiven van het interferentiepatroon, kan veroorzaken.
Het A-B effect is in wezen twee dimensionaal, en we kunnen dan een
gebonden toestand van een flux 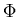 en een lading q beschouwen.
Als we dit flux-lading paar over een hoek
en een lading q beschouwen.
Als we dit flux-lading paar over een hoek 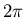 in het vlak draaien
zodat de beginsituatie terugkeert is de golffunctie veranderd met een
fasefactor
in het vlak draaien
zodat de beginsituatie terugkeert is de golffunctie veranderd met een
fasefactor
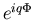 .
(voor een vlakke type II supergeleider hebben
we in principe
.
(voor een vlakke type II supergeleider hebben
we in principe
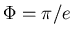 en q=e zodat de fasefactor -1 kan
worden). We kunnen dus aan deze fluxlading combinatie een spin
en q=e zodat de fasefactor -1 kan
worden). We kunnen dus aan deze fluxlading combinatie een spin
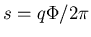 toekennen. Deze zal in het algemeen fractioneel zijn
en dat is in twee dimensies inderdaad een coinsistente mogelijkheid.
Het zelfde Aharonov-Bohm argument kan nu gebruikt worden om de
fasefactor te bepalen die een golffunctie van een systeem met twee
gelocaliseerde flux-lading combinaties krijgt, nadat de deeltjes
elkaar eenmaal omcirkelen. We vinden voor de combinaties
toekennen. Deze zal in het algemeen fractioneel zijn
en dat is in twee dimensies inderdaad een coinsistente mogelijkheid.
Het zelfde Aharonov-Bohm argument kan nu gebruikt worden om de
fasefactor te bepalen die een golffunctie van een systeem met twee
gelocaliseerde flux-lading combinaties krijgt, nadat de deeltjes
elkaar eenmaal omcirkelen. We vinden voor de combinaties
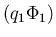 en
en
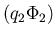 de fasefactor
de fasefactor
zodat we voor identieke paren vinden dat
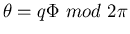 .
Dat wil zeggen dat ook de statistische parameter
.
Dat wil zeggen dat ook de statistische parameter 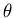 een willekeurige waarde kan aannemen, we spreken van een anyonen
omdat zij 'any phase' kunnen genereren onder verwisseling. Fermionen
en bosonen corresponderen dus met het geval
een willekeurige waarde kan aannemen, we spreken van een anyonen
omdat zij 'any phase' kunnen genereren onder verwisseling. Fermionen
en bosonen corresponderen dus met het geval
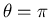 en
en
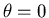 .
We hebben nu aannemelijk gemaakt dat een flux-lading
combinatie inderdaad een realisatie is van een deeltje met fractionele
spin en statistiek eigenschappen die voldoen aan het klassieke verband
.
We hebben nu aannemelijk gemaakt dat een flux-lading
combinatie inderdaad een realisatie is van een deeltje met fractionele
spin en statistiek eigenschappen die voldoen aan het klassieke verband
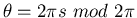 .
.
We gaan later in op het feit dat er ook niet-triviale
fasefactoren kunnen optreden bij het omcirkelen van niet-identieke
deeltjes, en die laten zien dat wat we `statistiek' noemen in het
algemeen de manifestatie is van een speciaal soort ' topologische'
wisselwerking tussen deeltjes.
We merken op dat het in twee dimensies mogelijk om een zogenaamde Chern-Simons theorie te definieren, dit is een theorie met een
ijkveld -een vectorpotentiaal- waarbij de bijbehorende electrische en
magnetische velden altijd nul zijn (er zijn dus geen fotonen mee
geassocieerd), behalve dan dat het automatisch de eerder geschetse
eigenschap realiseert, waarbij aan elke `lading' q een flux
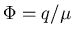 wordt toegevoegd, en
wordt toegevoegd, en 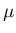 een parameter in het model
is. De enige fysische manifestatie van deze Chern-Simons potentialen
zijn dan Aharonov-Bohm fases, zo'n veld wordt dan ook een topologisch,
of statistisch ijkveld genoemd.
een parameter in het model
is. De enige fysische manifestatie van deze Chern-Simons potentialen
zijn dan Aharonov-Bohm fases, zo'n veld wordt dan ook een topologisch,
of statistisch ijkveld genoemd.
Het bewijs voor het verband tussen spin en statistiek is een van de
successen van de relativistische quantumveldentheorie, waar het
uiteindelijk terug te voeren is op Lorentzinvariantie, localiteit en
positiviteit van Hamiltoniaan. In de onderhavige discussie is het
verhelderend een alternatief, zeer aanschouwelijk bewijs te geven,
gebaseerd op een topologisch argument dat teruggaat naar Finkelstein.
Het amusante is dat dit bewijs in feite geen gebruik maakt van de
veldentheorie, hoewel we wel aannemen dat er voor elk
deeltjestype een type antideeltje bestaat (een toestand met
tegengestelde quantumgetallen , zodat deeltje en antideeltje kunnen
annihileren in de vacuumtoestand met triviale quantumgetallen). We
representeren een deeltje door een pijltje, en de wereldlijn van een
deeltje dat zijn pad in de tijd beschrijft wordt dan voorgesteld door
een lint, met een gemarkeerde rand (positie van de pijlpunt)
waardoor het mogelijk is om een voor- en een achterkant van het lint
te onderscheiden. Een antideeltje wordt voorgesteld door het
spiegelbeeld van het lint, d.w.z. we verwisselen voor en achterkant
maar behouden pijlorientatie, deze voorstelling impliceert dat een
gesloten lus van een lint in de ruimtetijd de creatie- en daaropvolgende
annihilatie van een deeltje-antideeltje paar voorstelt. Met deze
ingrediënten kunnen we ook een rotatie van het deeltje over een hoek
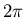 voorstellen door een volle twist van het lint, en
vanzelfsprekend ook de verwisseling van identieke deeltjes door twee
(identieke) linten te kruisen. Het conventionele verband tussen
spin en statistiek is dan de uitspraak dat de twee lintconfiguraties
in Figuur 1 topologisch equivalent zijn, dat dit zo is kan men
eenvoudig verifiëren met een broekriem. De linkerfiguur beschrijft
de creatie van twee paren, de verwisseling van de deeltjes en tot slot
de annihilatie van de nieuwe paren. De rechter figuur beschrijft de
creatie van een paar, gevolgd door een rotatie van het deeltje over
een hoek van
voorstellen door een volle twist van het lint, en
vanzelfsprekend ook de verwisseling van identieke deeltjes door twee
(identieke) linten te kruisen. Het conventionele verband tussen
spin en statistiek is dan de uitspraak dat de twee lintconfiguraties
in Figuur 1 topologisch equivalent zijn, dat dit zo is kan men
eenvoudig verifiëren met een broekriem. De linkerfiguur beschrijft
de creatie van twee paren, de verwisseling van de deeltjes en tot slot
de annihilatie van de nieuwe paren. De rechter figuur beschrijft de
creatie van een paar, gevolgd door een rotatie van het deeltje over
een hoek van 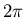 ,
waarna het paar tenslotte weer annihileert. We
hebben dus laten zien dat de actie van verwisseling hetzelfde effect
heeft als een rotatie over een hoek
,
waarna het paar tenslotte weer annihileert. We
hebben dus laten zien dat de actie van verwisseling hetzelfde effect
heeft als een rotatie over een hoek 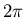 .
We zien trouwens ook dat
de spin van een deeltje en antideeltje gelijk moeten zijn, omdat de twist
in de rechterfiguur ook naar het antideeltjeslint geschoven kan
worden.
.
We zien trouwens ook dat
de spin van een deeltje en antideeltje gelijk moeten zijn, omdat de twist
in de rechterfiguur ook naar het antideeltjeslint geschoven kan
worden.
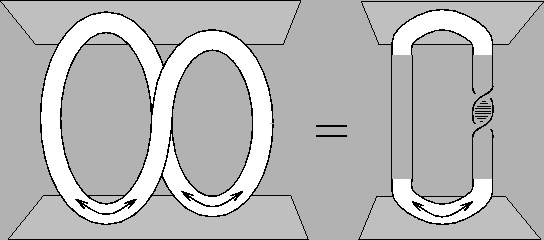
Figuur 1:
Het topologisch argument voor het kanonieke verband
tussen spin en statistiek. Het linker lint diagram beschrijft de
creatie van twee paren, gevolgt door verwisseling van de identieke
deeltjes waarna de nieuwe paren ieder weer annihileren. Dit diagram
kan continu veranderd worden het rechter diagram dat de creatie
beschrijft van een enkel paar waarna het deeltje (of het antideeltje)
gedraaid wordt over 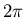 alvorens weer te annihileren. Dit verband
kan met een broekriem geverifieerd worden.
alvorens weer te annihileren. Dit verband
kan met een broekriem geverifieerd worden.
 |
In de Amsterdamse theoriegroep is er onderzoek gedaan naar de
mogelijkheid om de hierboven beschreven connecties nog verder te
generaliseren. En aangezien de fysische realisatie van flux-lading
combinaties bepaald niet onrealistisch zijn, is de vraag naar
niet-abelse generalisaties interessant. Niet abelse-fluxen
doen zich bijvoorbeeld voor in biaxiale nematische kristallen. In het
hier beschreven werk wordt een algemene oplossing gegeven voor de
situatie waar een niet-abelse ijkgroep gebroken wordt naar een
niet-abelse discrete ijkgroep. Er bestaan dan net zoals in de type II
supergeleider, stabiele magnetische vortices die nu echter niet-abelse
quantumgetallen dragen, hetgeen de situatie aanzienlijk compliceert.
Kenmerkend voor de niet-abelse (d.w.z. niet-commutatieve) ijktheorie
is dat de electrische en magnetisch velden - en dus ook de
vectorpotentiaal - matrix ( of Lie algebra) waardig zijn,
d.w.z. meerdere componenten hebben. Omdat matrices in het algemeen
niet commutatief zijn ( d.w.z. dat het matrixproduct AB niet gelijk
is aan BA) is de structuur van deze theorieën gecompliceerd. In de
theorieën die we beschouwen heeft de magnetische flux en de
electrisch lading dus ook meerdere componenten. De Aharonov-Bohm
fasefactor - nu de exponent van de Lie algebra waardige
vectorpotentiaal - neemt dan (per definitie) een waarde aan in de
corresponderende Lie groep. Kort gezegd niet-abelse fluxen
corresponderen met niet-commuterende groepselementen die samen een
(discrete) groep vormen. We kunnen deze fluxen laten versmelten (`fuseren') waarbij we de corresponderende groepselementen moeten
vermenigvuldigen om die van de nieuwe gecombineerde flux te verkrijgen
(waarbij de volgorde balangrijk is) (figuur 2a). Een eerste
`niet-triviale' fysische consequentie is een effect genaamd fluxmetamorfose, waarbij fluxen van identiteit veranderen als zij om
elkaar heen draaien. Uit figuur 2b volgt dat wanneer we flux A en Bverwisselen de corresponderende groeps elementen moeten voldoen aan de
relatie
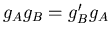 ,
zodat
,
zodat
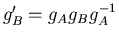 .
Als gA en gB niet commuteren is dus
.
Als gA en gB niet commuteren is dus
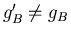 .
Dit laat zien dat deze fluxen een topologische
wisselwerking met elkaar hebben, die aanleiding geeft tot een niet-abels
Aharonov-Bohm effect.
.
Dit laat zien dat deze fluxen een topologische
wisselwerking met elkaar hebben, die aanleiding geeft tot een niet-abels
Aharonov-Bohm effect.
Figuur 2 (afwezig): Niet abelse fluxen. Het samengaan of fuseren van twee
fluxen (2a) en de eigenschap van fluxmetamorfose (2b).
Een tweede complicatie heeft te maken met de
beschrijving van de electrische ladingen en de restricties welke er
bestaan op de mogelijke flux-lading combinaties. Je kunt bewijzen dat
alleen die ladingen met een gegeven flux een paar kunnen vormen, als
de met de lading corresponderende matrix commuteert met de flux
matrix. De ladingen vormen aldus representaties van een specifieke
ondergroep van de oorspronkelijke groep die door alle fluxen wordt
gevormd.
Het probleem in zijn algemeenheid is nu om een taal te vinden waarin
de vragen over spin, statistiek, fusie , Aharonov-Bohm effecten bij
verstrooing, en de introductie van niet-abelse Chern-Simons
interacties, van de hier gedefinieerde niet abelse flux-lading
combinaties systematisch te beantwoorden zijn. Dit probleem kon
inderdaad volledig worden opgelost, mede omdat een nieuw soort
onderliggende symmetrie ontdekt werd. Deze symmetrie is een zogenaamde
quantumgroep, een soort verdubbeling van de groep die door de
fluxen wordt gegenereerd.
De situatie die ontstaat is dat alle fluxen, ladingen en mogelijke
combinaties daarvan, alle irreducibele representaties van de
quantumgroep vormen. Eén zo'n representatie kan dus meerdere
fluxen en ladingen kan bevatten zoals je in een niet abelse theorie
verwacht, aangezien matrices graag werken op vectoren. De toestanden
kunnen we beschrijven als
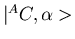 waarbij AC voor de fluxen
staat en
waarbij AC voor de fluxen
staat en 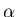 voor de bijbehorende ladingen. Voor zo'n gegeven
representatie kunnen we een unieke spinfactor
voor de bijbehorende ladingen. Voor zo'n gegeven
representatie kunnen we een unieke spinfactor
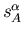 bepalen, deze
zijn vaak fractioneel.
bepalen, deze
zijn vaak fractioneel.
Er is een tensorrekening om flux-lading combinaties mee te `fuseren', die
doet denken aan het optellen van impulsmomenten in de gewone
quantummechanica. Deze heeft de vorm :
waarbij de constanten
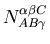 bepalen welke
representaties er in het fusieprodukt voorkomen en met welke
multipliciteit.
bepalen welke
representaties er in het fusieprodukt voorkomen en met welke
multipliciteit.
Om de vraag naar de statistiek te beantwoorden, blijkt de `lint
representatie' wederom zeer nuttig te zijn. De statistiek, d.w.z. de
fasefactor die men verkrijgt wanneer twee deeltjes (representaties dus)
elkaar omcirkelen, of die het gevolg is van het verwisselen van twee
identieke representaties, ligt niet voor de hand en blijkt nu direct af
te hangen van het fusiekanaal waar deze zich in bevinden. De factor
volgt uit het lintdiagram van figuur 3, dat een gegeneraliseerde
spin-statistiek connectie weergeeft. Het met de klok mee omcirkelen van
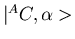 met
met
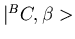 die samen in een toestand
die samen in een toestand
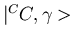 zitten geeft een factor
zitten geeft een factor
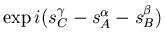 .
Het conventionele verband tussen spin en statistiek vinden
we terug in de bovenstaande situatie waarbij we een deeltje en
antideeltje in het vacuumkanaal laten fuseren.
.
Het conventionele verband tussen spin en statistiek vinden
we terug in de bovenstaande situatie waarbij we een deeltje en
antideeltje in het vacuumkanaal laten fuseren.
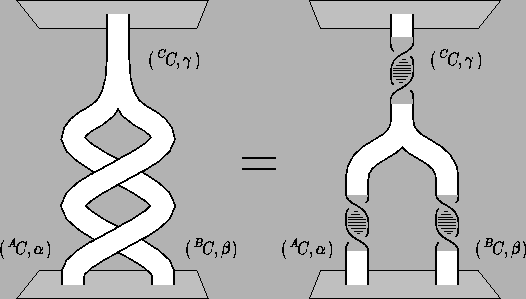
Figuur 3:
Het gegeneraliseerde verband tussen spin en statistiek.
Wanneer twee flux-lading combinaties elkaar in een gegeven fusie
kanaal omcirkelen (linker afbeelding), is dat topologisch equivalent
aan een operatie waarbij ieder van die deeltjes over een hoek 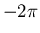 en het gefuseerde deeltje over een hoek
en het gefuseerde deeltje over een hoek 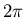 wordt gedraaid (rechter
afbeelding). Voor directe verificatie is een broek met lange pijpen
voldoende.
wordt gedraaid (rechter
afbeelding). Voor directe verificatie is een broek met lange pijpen
voldoende.
 |
Met het kennen van de geëigende representaties, de tensorproduct of
fusie regels voor die representaties, en de vlechteigenschappen
(verwisselingsrelaties), blijkt een elegante formulering van elk
fysisch probleem aangaande deze niet-abelse anyonen te
bestaan. Waarbij we denken aan verstrooiings processen maar ook aan
fraaie variaties op het thema van Einstein-Rosen-Podolski.
Toepassingen van de hier ontwikkelde technieken liggen voor de hand in
alle situaties waar collectieve excitaties (zoals defecten)
topologische wisselwerkingen met elkaar hebben, en dat is het geval
wanneer een medium in een fase met gebroken symmetrie zit. In drie
dimensies gaat het dan vaak over dyonen (dragers van zowel
electrische als magnetische lading) en in twee dimensies over
gecombineerde flux-lading dragers. Deze spelen een belangrijke rol in
het fractionele quantum Hall effect. Een intrigerende suggestie die
van dit onderzoek uitgaat is dat het verschil tussen fermionen en
bosonen hebben uiteindelijk een geometrische oorsprong
heeft. Buitengewoon interessant zijn ook de situaties waarbij de
residuele, ongebroken symmetriegroep van het medium niet-abels is. Dit
is het geval in diverse fasen van superfluide Helium, nematische fasen
van vloeibare kristallen, (2+1)-dimensionale gravitatie, Alice
electrodynamica (in 2 en 3 dimensies) enz. De hier beschreven methoden
kunnen ook een rol spelen in de formulering van zogenaamde
electrisch-magnetische dualiteiten in de veldentheorie,
d.w.z. de afbeelding van theorieën op elkaar of zichzelf, onder
verwisseling van de magnetische en electrische eigenschappen van de
theorie.